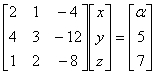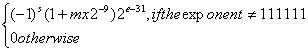1. Let (S, £ ) be a partial order with two minimal elements a and b, and a maximum element c. Let P : S ® {True, False} be a predicate defined on S. Suppose that p(a) = True, P(b) = False and P(x) Þ P(y) for all x, y Î S satisfying x £ y, where Þ stands for logical implication. Which of the following statements CANNOT be true?

(a) P(x) = True for all X Î S such that x ¹ b

(b) P(x) = False for all X Î S such that x ¹ a and x ¹ c

(c) P(x) = False for all X Î S such that b £ x and x ¹ c

(d) P(x) = False for all X Î S such that a £ and b £ x

2. Which of the following is a valid first order formula? (Here a and b are first order formulae with x as their only free variable)

(a) (( " x) [ a ] Þ ( " x)[ b ]) Þ ( " x) [ a Þ b ]

(b) ( " x) [ a ] Þ ( $ x) [ a Ù b ]

(c) (( " x) [ a v b ] Þ ( $ x)[ a ]) Þ ( " x) [ a ]

(d) ( " x) [ a Þ b ] Þ (( " x)[ a ] Þ ( " x) [ b ])

3. Consider the following formula a and its two interpretations I 1 and I 2

a: ( " x) [P x Û ( " y) [Q xy Û Ø Q yy]] ==> ( " x) [ Ø P x]

I 1: Domain: the set of natural numbers

P x == 'x is a prime number

Q xy == 'y divides x'

I 2: same as I 2 except that Px = 'x is a composite number'.

Which of the following statements is true?

(a) I 1 satisfies a , I 2 does not

(b) I 2 satisfies a , I 1 does not

(c) Neither I 1 nor I­ 2 satisfies a

(d) Both I 1 and I 2 satisfy a

4. m identical balls are to be placed in n distinct bags. You are given that m ³ kn, where k is a natural number ³ 1. In how many ways can the balls be placed in the bags if each bag must contain at least k balls?

(a)

(b)

(c)

(d)

5. Consider the following recurrence relation

T(1) = 1

T(n + 1) = T(n) + for all n ³ 1

The value of T(m 2) for m ³ 1 is

(a)

(b)

(c)

(d)

6. How many perfect matchings are there in a complete graph of 6 vertices?

• 15
• 24
• 30
• 60

7. Let f: A ® B be an injective (one-to-one) function. Define g: 2 A ® 2 B as:

g(C) = (f(x) \x Î C}, for all subsets C of A.

Define h: 2 B ® 2 A as: h(D) = { x\x Î A, f(x) Î D}, for all subsets D of B.

Which of the following statements is always true?

• g(h(D)) Í D
• g(h(D)) Ê D
• g(h(D)) Ç D = f
• g(h(D)) Ç (B-D) ¹ f

8. Consider the set {a, b, c} with binary operators + and x defined as follows:

+ a b c x a b c

a b a c a a b c

b a b c b b c a

c a c b c c c b

For example, a + c = c, c + a = a, c x b = c and b x c = a. Given the following set of equations:

(a x x)+(a x y)=c

(b x x)+(c x y)=c

the number of solution(s) (i.e., pair(s) (x, y) that satisfy the equations) is

(a) 0 (b) 1

(c) 2 (d) 3

9. Let å = (a, b, c, d, e) be an alphabet. We define an encoding scheme as follows:

g(a) = 3, g(b) = 5, g(c) = 7, g(d) = 9, g(e) = 11.

Let P i denote the i-th prime number (p 1 = 2)

For a non-empty string s = a 1...a n where each a i Î å , define f(s) = Õ n i= 1p i g(ai). For

a non-empty sequence (< Sl…Sn>) of strings from å + , define

h(<s l…s n>) = Õ n i = 1 p i f(si)

Which of the following numbers is the encoding, h of a non-empty sequence of strigs ?

• 2 73 75 7
• 2 83 85 8
• 2 93 95 9
• 2 105 107 10

10. A graph G = (V,E) satisfies | E | £ 3 | V | - 6. The min-degree of G is defined as

min {degree (v)}. Therefore, min-degree of G cannot be

v Î V

• 3
• 4
• 5
• 6

11. Consider the following system of linear equations

Notice that the second and the third columns of the coefficient matrix are linearly dependent. For how many values of a , does this system of equations have infinitely many solutions?

• 0
• 1
• 2
• infinitely many

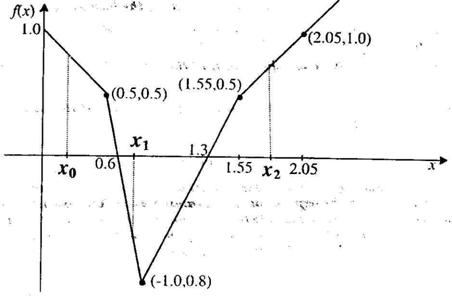
12. A piecewise linear function f(x) is plotted using thick solid lines in the figure below (the plot is drawn to scale).

I f we use the Newton-Raphson method to find the roots of f(x) = 0 using x 0, x 1 and x 2 respectively as initial guesses, the roots obtained would be

(a) 1.3, 0.6, and 0.6 respectively

(b) 0.6, 0.6, and 1.3respectively

(c) 1.3, 1.3, and 0.6 respectively

(d) 1.3,0.6, and 1.3 respectively

13. The following is a scheme for floating point number representation using 16 bits.

Bit Position 15 14 … … 9 8 … … … 0

Sign Exponent Mantissa

Let s, e, and m be the numbers represented in binary in the sign, exponent, and mantissa fields respectively. Then the floating point number represented is:

What is the maximum difference between two successive real numbers representable in this system?

• 2 –40
• 2-9
• 2 22
• 2 31

14. A 1-input, 2-output synchronous sequential circuit behaves as follows:

Let Z k n k denote the number of O's and 1's respectively in initial k bits of the input

(Z k + n k = k). The circuit outputs 00 until one of the following conditions holds.

• Z k – n k = 2. In this case, the output at the k-th and all subsequent clock ticks Is 10
• N k – Z k = 2. In this case, the output at the k-th and all subsequent clock ticks is 01.

What is the minimum number of states required in the state transition graph of the above circuit? ­

• 5
• 6
• 7
• 8

15. The literal count of a boolean expression is the sum of the number of times each literal appears in the expression. For example, the literal count of (xy + xz') is 4. What are the minimum possible literal counts of the product-or-sum and sum-of ­product representations respectively of the function given by the following Karnaugh map? Here, X denotes "don't care"

• (11, 9)
• (9, 13)
• (9, 10)
• (11, 11)