Print Page | Close Window

Gate Study Material-Algorithm

Printed From: One Stop GATE
Category: GATE AT A GLANCE
Forum Name: Other Discussions on GATE
Forum Discription: If you want to discuss some aspects of GATE which are not covered by any of the threads above, you are free to use this forum for those discussions.
URL: http://forum.onestopgate.com/forum_posts.asp?TID=960
Printed Date: 07Feb2025 at 12:25am


Topic: Gate Study Material-Algorithm
Posted By: Anamica
Subject: Gate Study Material-Algorithm
Date Posted: 04Apr2007 at 10:28pm

Concept of algorithm:


A common man’s belief is that a computer can do anything and everything that he imagines. It is very difficult to make people realize that it is not really the computer but the man behind computer who does everything.

In the modern internet world man feels that just by entering what he wants to search into the computers he can get information as desired by him. He believes that, this is done by computer. A common man seldom understands that a man made procedure called search has done the entire job and the only support provided by the computer is the executional speed and organized storage of information.

In the above instance, a designer of the information system should know what one frequently searches for. He should make a structured organization of all those details to store in memory of the computer. Based on the requirement, the right information is brought out. This is accomplished through a set of instructions created by the designer of the information system to search the right information matching the requirement of the user. This set of instructions is termed as program. It should be evident by now that it is not the computer, which generates automatically the program but it is the designer of the information system who has created this.

Thus, the program is the one, which through the medium of the computer executes to perform all the activities as desired by a user. This implies that programming a computer is more important than the computer itself while solving a problem using a computer and this part of programming has got to be done by the man behind the computer. Even at this stage, one should not quickly jump to a conclusion that coding is programming. Coding is perhaps the last stage in the process of programming. Programming involves various activities form the stage of conceiving the problem upto the stage of creating a model to solve the problem. The formal representation of this model as a sequence of instructions is called an algorithm and coded algorithm in a specific computer language is called a program.

One can now experience that the focus is shifted from computer to computer programming and then to creating an algorithm. This is algorithm design, heart of problem solving.


Characteristics of an algorithm


Let us try to present the scenario of a man brushing his own teeth(natural denture) as an algorithm as follows. Step 1. Take the brush Step 2. Apply the paste Step 3. Start brushing Step 4. Rinse Step 5. Wash Step 6. Stop If one goes through these 6 steps without being aware of the statement of the problem, he could possibly feel that this is the algorithm for cleaning a toilet. This is because of several ambiguities while comprehending every step. The step 1 may imply tooth brush, paint brush, toilet brush etc. Such an ambiguity doesn’t an instruction an algorithmic step. Thus every step should be made unambiguous. An unambiguous step is called definite instruction. Even if the step 2 is rewritten as apply the tooth paste, to eliminate ambiguities yet the conflicts such as, where to apply the tooth paste and where is the source of the tooth paste, need to be resolved. Hence, the act of applying the toothpaste is not mentioned. Although unambiguous, such unrealizable steps can’t be included as algorithmic instruction as they are not effective. The definiteness and effectiveness of an instruction implies the successful termination of that instruction. However the above two may not be sufficient to guarantee the termination of the algorithm. Therefore, while designing an algorithm care should be taken to provide a proper termination for algorithm. Thus, every algorithm should have the following five characteristic feature
    1. Input
      2.
    2. Output
      3.
    3. Definiteness
      4.
    4. Effectiveness
      5.
    5. Termination
Therefore, an algorithm can be defined as a sequence of definite and effective instructions, which terminates with the production of correct output from the given input. In other words, viewed little more formally, an algorithm is a step by step formalization of a mapping function to map input set onto an output set. The problem of writing down the correct algorithm for the above problem of brushing the teeth is left to the reader. For the purpose of clarity in understanding, let us consider the following examples. Example 1: Problem : finding the largest value among n>=1 numbers. Input : the value of n and n numbers Output : the largest value Steps :
    1. Let the value of the first be the largest value denoted by BIG
      2.
    2. Let R denote the number of remaining numbers. R=n-1
      3.
    3. If R != 0 then it is implied that the list is still not exhausted. Therefore look the next number called NEW.
      4.
    4. Now R becomes R-1
      5.
    5. If NEW is greater than BIG then replace BIG by the value of NEW
      6.
    6. Repeat steps 3 to 5 until R becomes zero.
      7.
    7. Print BIG
      8.
    8. Stop
End of algorithm Example 2: quadratic equation Example 3: listing all prime numbers between two limits n1 and n2.   1.2.1 Algorithmic Notations In this section we present the pseudocode that we use through out the book to describe algorithms. The pseudo code used resembles PASCAL and C language control structures. Hence, it is expected that the reader be aware of PASCAL/C. Even otherwise atleast now it is required that the reader should know preferably C to practically test the algorithm in this course work. However, for the sake of completion we present the commonly employed control constructs present in the algorithms.
  1. A conditional statement has the following form
    2.  If < condition> then Block 1 Else Block 2 If end. This pseudocode executes block1 if the condition is true otherwise block2 is executed.
  2. The two types of loop structures are counter based and conditional based and they are as follows
    • For variable = value1 to value2 do
Block For end Here the block is executed for all the values of the variable from value 1 to value 2.
    • There are two types of conditional looping, while type and repeat type.
While (condition) do Block While end. Here block gets executed as long as the condition is true.
    • Repeat
Block Until<condition> Here block is executed as long as condition is false. It may be observed that the block is executed atleast once in repeat type. Exercise 1; Devise the algorithm for the following and verify whether they satisfy all the features.
  1. An algorithm that inputs three numbers and outputs them in ascending order.
    2.
  2. To test whether the three numbers represent the sides of a right angle triangle.
    3.
  3. To test whether a given point p(x,y) lies on x-axis or y-axis or in I/II/III/IV quadrant.
    4.
  4. To compute the area of a circle of a given circumference
    5.
  5. To locate a specific word in a dictionary.

Numerical algorithm


If there are more then one possible way of solving a problem, then one may think of more than one algorithm for the same problem. Hence, it is necessary to know in what domains these algorithms are applicable. Data domain is an important aspect to be known in the field of algorithms. Once we have more than one algorithm for a given problem, how do we choose the best among them? The solution is to devise some data sets and determine a performance profile for each of the algorithms. A best case data set can be obtained by having all distinct data in the set. But, it is always complex to determine a data set, which exhibits some average behavior. The following sections give a brief idea of the well-known accepted algorithms.

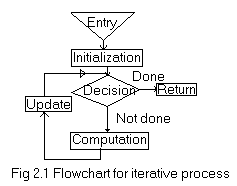
2.1 Numerical Algorithms Numerical analysis is the theory of constructive methods in mathematical analysis. Constructive method is a procedure used to obtain the solution for a mathematical problem in finite number of steps and to some desired accuracy. 2.1.1 Numerical Iterative Algorithm An iterative process can be illustrated with the flow chart given in fig 2.1. There are four main blocks in the process viz., initialization, decision, computation, and update. The functions of these four blocks are as follows:
    1. Initialization: all parameters are set to their initial values.
    2. Decision: decision parameter is used to determine when to exit from the loop.
    3. Computation: required computation is performed.
    4. Update: decision parameter is updated and is transformed for next iteration.
Many problems in engineering or science need the solution of simultaneous linear algebraic equations. Every iterative algorithm is infinite step algorithm. One of the iterative algorithms to solve system of simultaneous equations is Guass Siedel. This iteration method requires generally a few iteration. Iterative techniques have less round-off error. For large system of equations, the iteration required may be quite large. But, there is a guarantee of getting the convergent result. For example: consider the following set of equations, 10x1+2x2+x3= 9 2x1+20x2-2x3= -44 -2x1+3x2+10x3= 22. To solve the above set of equations using Guass Siedel iteration scheme, start with (x1(1),x2(1),x3(1))=(0,0,0) as initial values and compute the values of we write the system of x1, x2, x3 using the equations given below   x1(k+1)=(b1-a12x2(k+1)-a13x3(k))/a11 x2(k+1)=(b2-a21x1(k+1)-a23x3(k))/a22 x3(k+1)=(b3-a31x1(k+1)-a32x3(k+1))/a33 for k=1,2,3,… This process is continued upto some desired accuracy. Numerical iterative methods are also applicable for obtaining the roots of the equation of the form f(x)=0. The various iterative methods used for this purpose are,
    1. Bisection method: xi+2=(xi+xi+1)/2
    2. Regula- Falsi method: x2=(x0f(x1)+ x1f(x0))/ (f(x1)-f(x0))
    3. Newton Raphson method: x2= x1-f(x1)/f1(x1)


Print Page | Close Window