Heaps and Heap Sort
Printed From: One Stop GATE
Category: GATE Technical Discussions
Forum Name: GATE CS
Forum Discription: General Technical Discussions, Queries, doubts etc. for GATE in CS.
URL: http://forum.onestopgate.com/forum_posts.asp?TID=1103
Printed Date: 14Feb2025 at 7:42am
Topic: Heaps and Heap Sort
Posted By: gita
Subject: Heaps and Heap Sort
Date Posted: 08Apr2007 at 11:24pm
7.4 Heaps and Heap sort:
A heap is a complete binary tree with the property that the value at each node is atleast as large as the value at its children.
The
definition of a max heap implies that one of the largest elements is at
the root of the heap. If the elements are distinct then the root
contains the largest item. A max heap can be implemented using an array
an[ ].
To
insert an element into the heap, one adds it "at the bottom" of the
heap and then compares it with its parent, grandparent, great
grandparent and so on, until it is less than or equal to one of these
values. Algorithm insert describes this process in detail.
Algorithm Insert(a,n)
{
// Insert a[n] into the heap which is stored in a[1:n-1]
I=n;
item=a[n];
while( (I>n) and (a[ I!/2 ] < item)) do
{
a = a[I/2];
I=I/2;
}
a=item;
return (true);
}
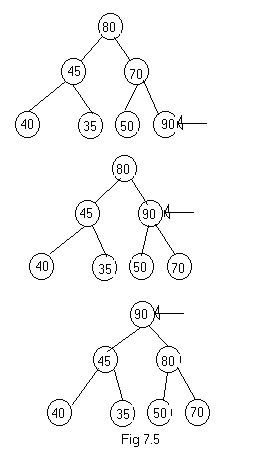The
figure shows one example of how insert would insert a new value into an
existing heap of five elements. It is clear from the algorithm and the
figure that the time for insert can vary. In the best case the new
elements are correctly positioned initially and no new values need to
be rearranged. In the worst case the number of executions of the while
loop is proportional to the number of levels in the heap. Thus if there
are n elements in the heap, inserting new elements takes O(log n) time
in the worst case.
To
delete the maximum key from the max heap, we use an algorithm called
Adjust. Adjust takes as input the array a[ ] and integer I and n. It
regards a[1..n] as a complete binary tree. If the subtrees rooted at 2I
and 2I+1 are max heaps, then adjust will rearrange elements of a[ ]
such that the http://www.vyomworld.com/gate/cs/ada/7.4.asp# - Algorithm Adjust(a,I,n)
{
j=2I;
item=a;
while (j<=n) do
{
if ((j<=n) and (a[j]< a[j+1])) then
j=j+1;
|