
 Active Topics
Active Topics  Memberlist
Memberlist  Calendar
Calendar  Search
Search  |
 Active Topics Active Topics  Memberlist Memberlist  Calendar Calendar  Search Search |
| |
| |
  |
| Author | Message |
|
sumana
Newbie 
Joined: 08Apr2007 Online Status: Offline Posts: 9 |
  Topic: Matrix Representation of graph Topic: Matrix Representation of graphPosted: 08Apr2007 at 10:18pm |
|
3.2 Matrix Representation of Graphs
Although a pictorial representation of a graph is very convenient
for a visual study, other representations are better for computer
processing. A matrix is a convenient and useful way of representing a
graph to a computer. Matrices lend themselves easily to mechanical
manipulations. Besides, many known results of matrix
algebra can be readily applied to study the structural properties of
graphs from an algebraic point of view. In many applications of graph
theory, such as in electrical network analysis and operation research,
matrices also turn out to be the natural way of expressing the problem.
3.2.1 Incidence Matrix
Let G be a graph with n vertices, e edges, and no self-loops. Define an n by e matrix A =[aij], whose n rows correspond to the n vertices and the e columns correspond to the e edges, as follows:
The matrix element
Aij = 1, if jth edge ej is incident on ith vertex vi, and
= 0, otherwise.
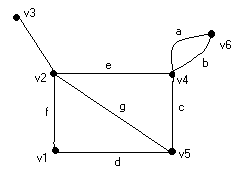
v1 0 0 0 1 0 1 0 0 v2 0 0 0 0 1 1 1 1 v3 0 0 0 0 0 0 0 1 v4 1 1 1 0 1 0 0 0 v5 0 0 1 1 0 0 1 0 v6 1 1 0 0 0 0 0 0 (b) Fig. 3-4 Graph and its incidence matrix. Such a matrix A is called the vertex-edge incidence matrix, or simply incidence matrix. Matrix A for a graph G is sometimes also written as A(G). A graph and its incidence matrix are shown in Fig. 3-4. The incidence matrix contains only two elements, 0 and 1. Such a matrix is called a binary matrix or a (0, 1)-matrix. The following observations about the incidence matrix A can readily be made:
Post Resume: Click here to Upload your Resume & Apply for Jobs |
|
 IP Logged IP Logged |
|
  |
||
Forum Jump |
You cannot post new topics in this forum You cannot reply to topics in this forum You cannot delete your posts in this forum You cannot edit your posts in this forum You cannot create polls in this forum You cannot vote in polls in this forum |
|
|

© Vyom Technosoft Pvt. Ltd. All Rights Reserved.