
 Active Topics
Active Topics  Memberlist
Memberlist  Calendar
Calendar  Search
Search  |
 Active Topics Active Topics  Memberlist Memberlist  Calendar Calendar  Search Search |
| |
 Topic: Gate Study Material Graph theory and related data Topic: Gate Study Material Graph theory and related data |
  |
| Author | Message | ||
|
Anamica
Newbie 
Joined: 04Apr2007 Online Status: Offline Posts: 9 |
  Topic: Gate Study Material Graph theory and related data Topic: Gate Study Material Graph theory and related dataPosted: 04Apr2007 at 10:37pm |
||
3.2 Matrix Representation of Graphs Although a pictorial representation of a graph is very convenient for a visual study, other representations are better for computer processing. A matrix is a convenient and useful way of representing a graph to a computer. Matrices lend themselves easily to mechanical manipulations. Besides, many known results of matrix algebra can be readily applied to study the structural properties of graphs from an algebraic point of view. In many applications of graph theory, such as in electrical network analysis and operation research, matrices also turn out to be the natural way of expressing the problem. 3.2.1 Incidence Matrix Let G be a graph with n vertices, e edges, and no self-loops. Define an n by e matrix A =[aij], whose n rows correspond to the n vertices and the e columns correspond to the e edges, as follows: The matrix element Aij = 1, if jth edge ej is incident on ith vertex vi, and = 0, otherwise.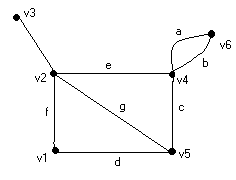
v1 0 0 0 1 0 1 0 0 v2 0 0 0 0 1 1 1 1 v3 0 0 0 0 0 0 0 1 v4 1 1 1 0 1 0 0 0 v5 0 0 1 1 0 0 1 0 v6 1 1 0 0 0 0 0 0 (b) Fig. 3-4 Graph and its incidence matrix. Such a matrix A is called the vertex-edge incidence matrix, or simply incidence matrix. Matrix A for a graph G is sometimes also written as A(G). A graph and its incidence matrix are shown in Fig. 3-4. The incidence matrix contains only two elements, 0 and 1. Such a matrix is called a binary matrix or a (0, 1)-matrix. The following observations about the incidence matrix A can readily be made: 3.3 Trees The concept of a tree is probably the most important in graph theory, especially for those interested in applications of graphs. A tree is a connected graph without any circuits. The graph in Fig 3-5 for instance, is a tree. It follows immediately from the definition that a tree has to be a simple graph, that is, having neither a self-loop nor parallel edges (because they both form circuits).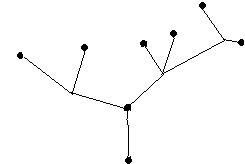 Fig. 3-5. Tree
Trees appear in numerous instances. The
genealogy of a family is often represented by means of a tree. A river
with its tributaries and sub-tributaries can also be represented by a
tree. The sorting of mail according to zip code and the sorting of
punched cards are done according to a tree (called decision tree or sorting tree).
3.3.1 Some properties of Trees
Fig. 3-5. Tree
Trees appear in numerous instances. The
genealogy of a family is often represented by means of a tree. A river
with its tributaries and sub-tributaries can also be represented by a
tree. The sorting of mail according to zip code and the sorting of
punched cards are done according to a tree (called decision tree or sorting tree).
3.3.1 Some properties of Trees
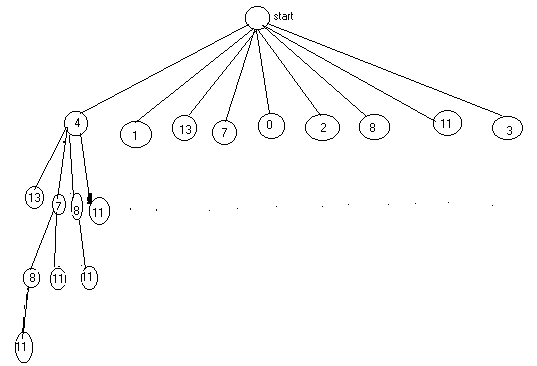 Fig. 3-6 Tree of a monotonically increasing sequences in 4,1,13,7,0,2,8,11,3
3.3.2 Pendent Vertices in a Tree
It
is observed that a tree shown in the Fig. 3-5 has several pendant
vertices. A pendant vertex was defined as a vertex of degree one). The
reason is that in a tree of n vertices we have n-1 edges, and hence
2(n-1) degrees to be divided among n vertices. Since no vertex can be
of zero degree, we must have at least two vertices of degree one in a
tree. This makes sense only if n ³
2.
An Application: The following
problem is used in teaching computer programming. Given a sequence of
integers, no two of which are the same find the largest monotonically
increasing subsequence in it. Suppose that the sequence given to us is
4,1,13,7,0,2,8,11,3; it can be represented by a tree in which the
vertices (except the start vertex) represent individual numbers in the
sequence, and the path from the start vertex to a particular vertex v describes the monotonically increasing subsequence terminating in v.
As shown in Fig. 3-6, this sequence contains
four longest monotonically increasing subsequences, that is,
(4,7,8,11), (1,7,8,11), (1,2,8,11) and (0,2,8,11). Each is of length
four. Computer programmers refer to such a tree used in representing
data as a data tree.
3.3.3 Rooted and Binary Tree
A tree in which one vertex (called the root) is distinguished from all the others is called a rooted tree. For instance, in Fig. 3-6 vertex named start, is distinguished from the rest of the vertices. Hence vertex start can be considered the root of the tree, and so the tree is rooted. Generally, the term tree means trees without any root. However, for emphasis they are sometimes called free trees (or non rooted trees) to differentiate them from the rooted kind.
Fig. 3-6 Tree of a monotonically increasing sequences in 4,1,13,7,0,2,8,11,3
3.3.2 Pendent Vertices in a Tree
It
is observed that a tree shown in the Fig. 3-5 has several pendant
vertices. A pendant vertex was defined as a vertex of degree one). The
reason is that in a tree of n vertices we have n-1 edges, and hence
2(n-1) degrees to be divided among n vertices. Since no vertex can be
of zero degree, we must have at least two vertices of degree one in a
tree. This makes sense only if n ³
2.
An Application: The following
problem is used in teaching computer programming. Given a sequence of
integers, no two of which are the same find the largest monotonically
increasing subsequence in it. Suppose that the sequence given to us is
4,1,13,7,0,2,8,11,3; it can be represented by a tree in which the
vertices (except the start vertex) represent individual numbers in the
sequence, and the path from the start vertex to a particular vertex v describes the monotonically increasing subsequence terminating in v.
As shown in Fig. 3-6, this sequence contains
four longest monotonically increasing subsequences, that is,
(4,7,8,11), (1,7,8,11), (1,2,8,11) and (0,2,8,11). Each is of length
four. Computer programmers refer to such a tree used in representing
data as a data tree.
3.3.3 Rooted and Binary Tree
A tree in which one vertex (called the root) is distinguished from all the others is called a rooted tree. For instance, in Fig. 3-6 vertex named start, is distinguished from the rest of the vertices. Hence vertex start can be considered the root of the tree, and so the tree is rooted. Generally, the term tree means trees without any root. However, for emphasis they are sometimes called free trees (or non rooted trees) to differentiate them from the rooted kind.
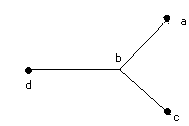 Fig. 3-6 Tree.
Binary Trees: A
special class of rooted trees, called binary rooted trees, is of
particular interest, since they are extensively used in the study of
computer search methods, binary identification problems, and
variable-length binary codes. A binary tree is defined as a
tree in which there is exactly one vertex of degree two, and each of
the remaining vertices of degree one or three. Since the vertex of
degree two is distinct from all other vertices, this vertex serves as a
root. Thus every binary tree is a rooted tree.
3.3.4 Spanning Trees
So far we have discussed the trees when it
occurs as a graph by itself. Now we shall study the tree as a subgraph
of another graph. A given graph has numerous subgraphs, from e edges, 2e
distinct combinations are possible. Obviously, some of these subgrphs
will be trees. Out of these trees we are particularly interested in
certain types of trees, called spanning trees.
A tree T is said to be a spanning tree of a
connected graph G if T is a subgraph of G and T contains all vertices
of G. Since the vertices of G are barely hanging together in a spanning
tree, it is a sort of skeleton of the original graph G. This is why a
spanning tree is sometimes referred to as a skeleton or scaffolding of G. Since spanning trees are the largest trees among all trees in G, it is also quite appropriate to call a spanning tree a maximal tree subgraph or maximal tree of G.
Finding a spanning tree of a connected graph G
is simple. If G has no circuit, it is its own spanning tree. If G has a
circuit, delete an edge from the circuit. This will still leave the
graph connected. If there are more circuits, repeat the operation till
an edge from the last circuit is deleted, leaving a connected,
circuit-free graph that contains all the vertices of G.
3.3.5 Hamiltonian Paths and Circuits
Hamiltonian circuit in a connected graph is defined as a closed walk that traverses every vertex
of G exactly once, except of course the starting vertex, at which the
walk also terminates. A circuit in a connected graph G is said to be
Hamiltonian if it includes every vertex of G. Hence a Hamiltonian
circuit in a graph of n vertices consists of exactly n edges.
Hamiltonian path: If we remove any one edge from a Hamiltonian circuit, we are left with a path. This path is called a Hamiltonian path.
Clearly, a Hamiltonian path in a graph G traverses every vertex of G.
Since a Hamiltonian path is a subgraph of a Hamiltonian circuit (which
in turn is a subgraph of another graph), every graph that has a
Hamiltonian circuit also has a Hamiltonian path. There are, however,
many graphs with Hamiltonian paths that have no Hamiltonian circuits.
The length of a Hamiltonian path in a connected graph of n vertices is
n-1.
3.3.5 Traveling-Salesman Problem
A problem closely related to the question of Hamiltonian circuits is the Traveling-salesman problem,
stated as follows: A salesman is required to visit a number of cities
during a trip. Given the distances between the cities, in what order
should he travel so as to visit every city precisely once and return
home, with the minimum mileage traveled?
Representing the cities by vertices and the roads between them by edges, we get a graph. In this graph, with every edge ei there is associated a real number (the distance in miles, say), w(ei). Such a graph is called a weighted graph; w(ei) being the weight of edge ei.
In our problem, if each of the cities has a road to every other city, we have a complete weighted graph. This graph has numerous Hamiltonian circuits, and we are to pick the one that has the smallest sum of distances (or weights).
The total number of different (not edge
disjoint, of course) Hamiltonian circuits in a complete graph of n
vertices can be shown to be (n-1)! / 2. This follows from the fact that
starting from any vertex we have n-1 edges to choose from the first
vertex, n-2 from the second, n-3 from the third, and so on. These being
independent, results with (n-1)! choices. This number is, however,
divided by 2, because each Hamiltonian circuit has been counted twice.
Theoretically, the problem of the traveling
salesman can always be solved by enumerating all (n-1)!/2 Hamiltonian
circuits, calculating the distance traveled in each, and then picking
the shortest one. However, for a large value of n, the labor involved
is too great even for a digital computer.
The problem is to prescribe a manageable
algorithm for finding the shortest route. No efficient algorithm for
problems of arbitrary size has yet been found, although many attempts
have been made. Since this problem has applications in operations
research, some specific large-scale examples have been worked out.
There are also available several heuristic methods of solution that
give a route very close to the shortest one, but do not guarantee the
shortest.
Exercise 3
Fig. 3-6 Tree.
Binary Trees: A
special class of rooted trees, called binary rooted trees, is of
particular interest, since they are extensively used in the study of
computer search methods, binary identification problems, and
variable-length binary codes. A binary tree is defined as a
tree in which there is exactly one vertex of degree two, and each of
the remaining vertices of degree one or three. Since the vertex of
degree two is distinct from all other vertices, this vertex serves as a
root. Thus every binary tree is a rooted tree.
3.3.4 Spanning Trees
So far we have discussed the trees when it
occurs as a graph by itself. Now we shall study the tree as a subgraph
of another graph. A given graph has numerous subgraphs, from e edges, 2e
distinct combinations are possible. Obviously, some of these subgrphs
will be trees. Out of these trees we are particularly interested in
certain types of trees, called spanning trees.
A tree T is said to be a spanning tree of a
connected graph G if T is a subgraph of G and T contains all vertices
of G. Since the vertices of G are barely hanging together in a spanning
tree, it is a sort of skeleton of the original graph G. This is why a
spanning tree is sometimes referred to as a skeleton or scaffolding of G. Since spanning trees are the largest trees among all trees in G, it is also quite appropriate to call a spanning tree a maximal tree subgraph or maximal tree of G.
Finding a spanning tree of a connected graph G
is simple. If G has no circuit, it is its own spanning tree. If G has a
circuit, delete an edge from the circuit. This will still leave the
graph connected. If there are more circuits, repeat the operation till
an edge from the last circuit is deleted, leaving a connected,
circuit-free graph that contains all the vertices of G.
3.3.5 Hamiltonian Paths and Circuits
Hamiltonian circuit in a connected graph is defined as a closed walk that traverses every vertex
of G exactly once, except of course the starting vertex, at which the
walk also terminates. A circuit in a connected graph G is said to be
Hamiltonian if it includes every vertex of G. Hence a Hamiltonian
circuit in a graph of n vertices consists of exactly n edges.
Hamiltonian path: If we remove any one edge from a Hamiltonian circuit, we are left with a path. This path is called a Hamiltonian path.
Clearly, a Hamiltonian path in a graph G traverses every vertex of G.
Since a Hamiltonian path is a subgraph of a Hamiltonian circuit (which
in turn is a subgraph of another graph), every graph that has a
Hamiltonian circuit also has a Hamiltonian path. There are, however,
many graphs with Hamiltonian paths that have no Hamiltonian circuits.
The length of a Hamiltonian path in a connected graph of n vertices is
n-1.
3.3.5 Traveling-Salesman Problem
A problem closely related to the question of Hamiltonian circuits is the Traveling-salesman problem,
stated as follows: A salesman is required to visit a number of cities
during a trip. Given the distances between the cities, in what order
should he travel so as to visit every city precisely once and return
home, with the minimum mileage traveled?
Representing the cities by vertices and the roads between them by edges, we get a graph. In this graph, with every edge ei there is associated a real number (the distance in miles, say), w(ei). Such a graph is called a weighted graph; w(ei) being the weight of edge ei.
In our problem, if each of the cities has a road to every other city, we have a complete weighted graph. This graph has numerous Hamiltonian circuits, and we are to pick the one that has the smallest sum of distances (or weights).
The total number of different (not edge
disjoint, of course) Hamiltonian circuits in a complete graph of n
vertices can be shown to be (n-1)! / 2. This follows from the fact that
starting from any vertex we have n-1 edges to choose from the first
vertex, n-2 from the second, n-3 from the third, and so on. These being
independent, results with (n-1)! choices. This number is, however,
divided by 2, because each Hamiltonian circuit has been counted twice.
Theoretically, the problem of the traveling
salesman can always be solved by enumerating all (n-1)!/2 Hamiltonian
circuits, calculating the distance traveled in each, and then picking
the shortest one. However, for a large value of n, the labor involved
is too great even for a digital computer.
The problem is to prescribe a manageable
algorithm for finding the shortest route. No efficient algorithm for
problems of arbitrary size has yet been found, although many attempts
have been made. Since this problem has applications in operations
research, some specific large-scale examples have been worked out.
There are also available several heuristic methods of solution that
give a route very close to the shortest one, but do not guarantee the
shortest.
Exercise 3
Post Resume: Click here to Upload your Resume & Apply for Jobs |
|||
 IP Logged IP Logged |
|||
  |
||
Forum Jump |
You cannot post new topics in this forum You cannot reply to topics in this forum You cannot delete your posts in this forum You cannot edit your posts in this forum You cannot create polls in this forum You cannot vote in polls in this forum |
|
|

© Vyom Technosoft Pvt. Ltd. All Rights Reserved.