4.1 Divide and Conquer
There are a
number of general and powerful computational strategies that are
repeatedly used in computer science. It is often possible to phrase any
problem in terms of these general strategies. These general strategies
are Divide and Conquer, Dynamic Programming. The techniques of Greedy
Search, Backtracking and Branch and Bound evaluation are variations of
dynamic programming idea. All these strategies and techniques are
discussed in the subsequent chapters.
The most widely known and often used of these is the divide and conquer strategy.
The basic idea
of divide and conquer is to divide the original problem into two or
more sub-problems which can be solved by the same technique. If it is
possible to split the problem further into smaller and smaller
sub-problems, a stage is reached where the sub-problems are small
enough to be solved without further splitting. Combining the solutions
of the individuals we get the final conquering. Combining need not
mean, simply the union of individual solutions.
Divide and Conquer involves four steps
- Divide
- Conquer [Initial Conquer occurred due to solving]
- Combine
- Conquer [Final Conquer].
In precise, forward journey is divide and backward journey is Conquer. A general binary divide and conquer algorithm is :
Procedure D&C (P,Q) //the data size is from p to q
{
If size(P,Q) is small Then
Solve(P,Q)
Else
M ¬
divide(P,Q)
Combine (D&C(P,M), D&C(M+1,Q))
}
Sometimes, this
type of algorithm is known as control abstract algorithms as they give
an abstract flow. This way of breaking down the problem has found wide
application in sorting, selection and searching algorithm.
4.1 Binary Search:
Algorithm:
m¬
(p+q)/2
If (p £
m £
q) Then do the following Else Stop
If (A(m) = Key Then ‘successful’ stop
Else
If (A(m) < key Then
q=m-1;
Else
p¬
m+1
End Algorithm.
Illustration :
Consider the data set with elements {12,18,22,32,46,52,59,62,68}. First let us consider the simulation for successful cases.
Successful cases:
Key=12 P Q m Search
1 9 5 x
1 4 2 x
1 1 1 successful
To search 12, 3 units of time is required
Key=18 P Q m Search
1 9 5 x
1 4 2 successful
To search 18, 2 units of time is required
Key=22 P Q m Search
1 9 5 x
1 4 2 x
3 4 3 successful
To search 22, 3 units of time is required
Key=32 P Q m Search
1 9 5 x
1 4 2 x
3 4 3 x
4 4 4 successful
To search 32, 4 units of time is required
Key=46 P Q m Search
1 9 5 successful
To search 46, 1 unit of time is required
Key=52 P Q m Search
1 9 5 x
6 9 7 x
6 6 6 successful
To search 52, 3 units of time is required
Key=59 P Q m Search
1 9 5 x
6 9 7 successful
To search 59, 2 units of time is required
Key=62 P Q m Search
1 9 5 x
6 9 7 x
8 9 8 successful
To search 62, 3 units of time is required
Key=68 P Q m Search
1 9 5 x
6 9 7 x
8 9 8 x
9 9 9 successful
To search 68, 4 units of time is required
3+2+3+4+1+3+2+4
Successful average search time= -------------------------
9
unsuccessful cases
Key=25 P Q m Search
1 9 5 x
1 4 2 x
3 4 3 x
4 4 4 x
To search 25, 4 units of time is required
Key=65 P Q m Search
1 9 5 x
6 9 7 x
8 9 8 x
9 9 9 x
To search 65, 4 units of time is required
4+4
Unsuccessful search time =--------------------
2
average (sum of unsuccessful search time
search = + sum of Successful search time)/(n+(n+1))
time
Study Notes Home | Next Section>>
4.1 Divide and Conquer
There are a
number of general and powerful computational strategies that are
repeatedly used in computer science. It is often possible to phrase any
problem in terms of these general strategies. These general strategies
are Divide and Conquer, Dynamic Programming. The techniques of Greedy
Search, Backtracking and Branch and Bound evaluation are variations of
dynamic programming idea. All these strategies and techniques are
discussed in the subsequent chapters.
The most widely known and often used of these is the divide and conquer strategy.
The basic idea
of divide and conquer is to divide the original problem into two or
more sub-problems which can be solved by the same technique. If it is
possible to split the problem further into smaller and smaller
sub-problems, a stage is reached where the sub-problems are small
enough to be solved without further splitting. Combining the solutions
of the individuals we get the final conquering. Combining need not
mean, simply the union of individual solutions.
Divide and Conquer involves four steps
- Divide
- Conquer [Initial Conquer occurred due to solving]
- Combine
- Conquer [Final Conquer].
In precise, forward journey is divide and backward journey is Conquer. A general binary divide and conquer algorithm is :
Procedure D&C (P,Q) //the data size is from p to q
{
If size(P,Q) is small Then
Solve(P,Q)
Else
M ¬
divide(P,Q)
Combine (D&C(P,M), D&C(M+1,Q))
}
Sometimes, this
type of algorithm is known as control abstract algorithms as they give
an abstract flow. This way of breaking down the problem has found wide
application in sorting, selection and searching algorithm.
4.1 Binary Search:
Algorithm:
m¬
(p+q)/2
If (p £
m £
q) Then do the following Else Stop
If (A(m) = Key Then ‘successful’ stop
Else
If (A(m) < key Then
q=m-1;
Else
p¬
m+1
End Algorithm.
Illustration :
Consider the data set with elements {12,18,22,32,46,52,59,62,68}. First let us consider the simulation for successful cases.
Successful cases:
Key=12 P Q m Search
1 9 5 x
1 4 2 x
1 1 1 successful
To search 12, 3 units of time is required
Key=18 P Q m Search
1 9 5 x
1 4 2 successful
To search 18, 2 units of time is required
Key=22 P Q m Search
1 9 5 x
1 4 2 x
3 4 3 successful
To search 22, 3 units of time is required
Key=32 P Q m Search
1 9 5 x
1 4 2 x
3 4 3 x
4 4 4 successful
To search 32, 4 units of time is required
Key=46 P Q m Search
1 9 5 successful
To search 46, 1 unit of time is required
Key=52 P Q m Search
1 9 5 x
6 9 7 x
6 6 6 successful
To search 52, 3 units of time is required
Key=59 P Q m Search
1 9 5 x
6 9 7 successful
To search 59, 2 units of time is required
Key=62 P Q m Search
1 9 5 x
6 9 7 x
8 9 8 successful
To search 62, 3 units of time is required
Key=68 P Q m Search
1 9 5 x
6 9 7 x
8 9 8 x
9 9 9 successful
To search 68, 4 units of time is required
3+2+3+4+1+3+2+4
Successful average search time= -------------------------
9
unsuccessful cases
Key=25 P Q m Search
1 9 5 x
1 4 2 x
3 4 3 x
4 4 4 x
To search 25, 4 units of time is required
Key=65 P Q m Search
1 9 5 x
6 9 7 x
8 9 8 x
9 9 9 x
To search 65, 4 units of time is required
4+4
Unsuccessful search time =--------------------
2
average (sum of unsuccessful search time
search = + sum of Successful search time)/(n+(n+1))
time
4.2 Max-Min Search
Max-Min search problem aims at finding the smallest as well as the biggest element in a vector A of n elements.
Following the steps of Divide and Conquer the vector can be divided into sub-problem as shown below.
The search has now reduced to comparison
of 2 numbers. The time is spent in conquering and comparing which is
the major step in the algorithm.
Algorithm: Max-Min (p, q, max, min)
{
If (p = q) Then
max = a(p)
min = a(q)
Else
If ( p – q-1) Then
If a(p) > a(q) Then
max = a(p)
min = a(q)
Else
max = a(q)
min = a(p)
If End
Else
m ¬
(p+q)/2
max-min(p,m,max1,min1)
max-min(m+1,q,max2,min2)
max ¬
large(max1,max2)
min ¬
small(min1,min2)
If End
If End
Algorithm End.
Illustration
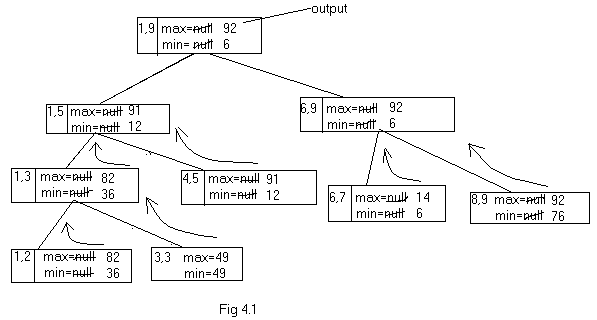 Consider a
data set with elements {82,36,49,91,12,14,06,76,92}. Initially the max
and min variables have null values. In the first call, the list is
broken into two equal halves.. The list is again broken down into two.
This process is continued till the length of the list is either two or
one. Then the maximum and minimum values are chosen from the smallest
list and these values are returned to the preceding step where the
length of the list is slightly big. This process is continued till the
entire list is searched. The detail description is shown in fig 4.1
Consider a
data set with elements {82,36,49,91,12,14,06,76,92}. Initially the max
and min variables have null values. In the first call, the list is
broken into two equal halves.. The list is again broken down into two.
This process is continued till the length of the list is either two or
one. Then the maximum and minimum values are chosen from the smallest
list and these values are returned to the preceding step where the
length of the list is slightly big. This process is continued till the
entire list is searched. The detail description is shown in fig 4.1
4.3 Integer multiplication
There are various methods of obtaining
the product of two numbers. The repeated addition method is left as an
assignment for the reader. The reader is expected to find the product
of some bigger numbers using the repeated addition method.
Another way of finding the product is the one we generally use i.e., the left shift method.
4.3.1 left shift method
981*1234
3924
2943*
1962**
981***
1210554
In this method, a=981 is the
multiplicand and b=1234 is the multiplier. A is multiplied by every
digit of b starting from right to left. On each multiplication the
subsequent products are shifted one place left. Finally the products
obtained by multiplying a by each digit of b is summed up to obtain the
final product.
The above product can also be obtained by a right shift method, which can be illustrated as follows,
4.3.2 right shift method
981*1234
981
1962
*2943
**3924
1210554
In the above method, a is multiplied by
each digit of b from leftmost digit to rightmost digit. On every
multiplication the product is shifted one place to the right and
finally all the products obtained by multiplying ‘a’ by each digit of
‘b’ is added to obtain the final result.
The product of two numbers can also be obtained by dividing ‘a’ and multiplying ‘b’ by 2 repeatedly until a<=1.
4.3.3 halving and doubling method
Let a=981 and b=1234
The steps to be followed are
- If a is odd store b
- A=a/2 and b=b*2
- Repeat step 2 and step 1 till a<=1
|
a |
b |
result |
|
981 |
1234 |
1234 |
|
490 |
2468 |
------------ |
|
245 |
4936 |
4936 |
|
122 |
9872 |
--------- |
|
61 |
19744 |
19744 |
|
30 |
39488 |
------------ |
|
15 |
78976 |
78976 |
|
7 |
157952 |
157952 |
|
3 |
315904 |
315904 |
|
1 |
631808 |
631808 |
Sum=1210554
The above method is called the halving and doubling method.
4.3.4 Speed up algorithm:
In this method we split the number till
it is easier to multiply. i.e., we split 0981 into 09 and 81 and 1234
into 12 and 34. 09 is then multiplied by both 12 and 34 but, the
products are shifted ‘n’ places left before adding. The number of
shifts ‘n’ is decided as follows
|
Multiplication sequence |
shifts |
|
|
09*12 |
4 |
108**** |
|
09*34 |
2 |
306** |
|
81*12 |
2 |
972** |
|
81*34 |
0 |
2754 |
Sum=1210554
For 0981*1234, multiplication of 34 and 81 takes zero shifts, 34*09 takes 2 shifts, 12 and 81 takes 2 shifts and so on.
Exercise 4
Write the algorithm to find the product of two numbers for all the methods explained. Hand simulate the algorithm for atleast 10 different numbers. Implement the same for verification. Write a program to find the maximum and minimum of the list of n element with and without using recursion.
Post Resume: Click here to Upload your Resume & Apply for Jobs |

 Active Topics
Active Topics  Memberlist
Memberlist  Calendar
Calendar  Search
Search 
 Active Topics
Active Topics  Memberlist
Memberlist  Calendar
Calendar  Search
Search  Topic: Gate Study Material data structure
Topic: Gate Study Material data structure



 Topic: Gate Study Material data structure
Topic: Gate Study Material data structure Consider a
data set with elements {82,36,49,91,12,14,06,76,92}. Initially the max
and min variables have null values. In the first call, the list is
broken into two equal halves.. The list is again broken down into two.
This process is continued till the length of the list is either two or
one. Then the maximum and minimum values are chosen from the smallest
list and these values are returned to the preceding step where the
length of the list is slightly big. This process is continued till the
entire list is searched. The detail description is shown in fig 4.1
Consider a
data set with elements {82,36,49,91,12,14,06,76,92}. Initially the max
and min variables have null values. In the first call, the list is
broken into two equal halves.. The list is again broken down into two.
This process is continued till the length of the list is either two or
one. Then the maximum and minimum values are chosen from the smallest
list and these values are returned to the preceding step where the
length of the list is slightly big. This process is continued till the
entire list is searched. The detail description is shown in fig 4.1 IP Logged
IP Logged

