
 Active Topics
Active Topics  Memberlist
Memberlist  Calendar
Calendar  Search
Search  |
 Active Topics Active Topics  Memberlist Memberlist  Calendar Calendar  Search Search |
| |
| |
  |
| Author | Message |
|
gita
Newbie 
Joined: 08Apr2007 Online Status: Offline Posts: 19 |
  Topic: Backtracking Topic: BacktrackingPosted: 08Apr2007 at 10:56pm |
|
6.1 Backtracking
Problems, which deal with searching a set of solutions, or which
ask for an optimal solution satisfying some constraints can be solved
using the backtracking formulation. The backtracking algorithm yields
the proper solution in fewer trials.
The basic idea of backtracking is to build up a vector one component at
a time and to test whether the vector being formed has any chance of
success. The major advantage of this algorithm is that if it is
realized that the partial vector generated does not lead to an optimal
solution then that vector may be ignored.
Backtracking algorithm determine the solution by systematically
searching the solution space for the given problem. This search is
accomplished by using a free organization. Backtracking is a depth
first search with some bounding function. All solutions using
backtracking are required to satisfy a complex set of constraints. The
constraints may be explicit or implicit.
Explicit constraints are rules, which restrict each vector element to
be chosen from the given set. Implicit constraints are rules, which
determine which of the tuples in the solution space, actually satisfy
the criterion function.
6.1.1 Cassette filling problem:
There are n programs that are to be stored on a tape of length L. Every program ‘i’ is of length li.
All programs can be stored on the tape if and only if the sum of the
lengths of the programs is at most L. In this problem, it is assumed
that whenever a program is to be retrieved, the tape is positioned at
the start end. Hence, the time tj needed to retrieve program ij from a tape having the programs in the order i1,i2, …,in is called mean retrieval time(MRT) and is given by
tj =S
lik k=1,2,…,j
In the optimal storage
on tape problem, we are required to find a permutation for the n
programs so that when they are stored on the tape, the MRT is minimized.
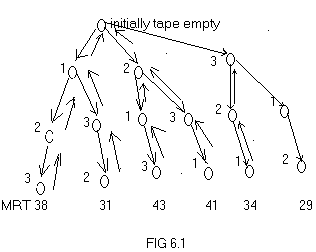
Let n=3 and (l1,l2,l3)=(5,10,3),there are n!=6 possible orderings. These orderings and their respective MRT is given in the fig 6.1. Hence, the best order of recording is 3,1,2.
 6.1.2 Subset problem:
There are n positive numbers given in a set. The desire is to find all
possible subsets of this set, the contents of which add onto a
predefined value M.
Let there be n elements in the main set. W=w[1..n] represent the
elements of the set. i.e., w = (w1,w2,w3,…,wn) vector x = x[1..n]
assumes either 0 or 1 value. If element w(i) is included in the subset
then x(i) =1.
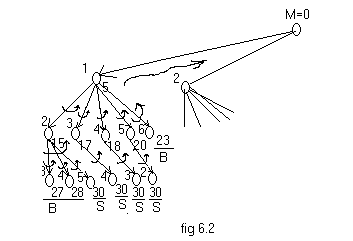
Consider n=6 m=30 and w[1..6]={5,10,12,13,15,18}. The partial
backtracking tree is shown in fig 6.2. The label to the left of a node
represents the item number chosen for insertion and the label to the
right represents the space occupied in M. S represents a solution to
the given problem and B represents a bounding criteria if no solution
can be reached. For the above problem the solution could be
(1,1,0,0,1,0), (1,0,1,1,0,0) and (0,0,1,0,0,1). Completion of the tree structure is left as an assignment for the reader.
6.1.2 Subset problem:
There are n positive numbers given in a set. The desire is to find all
possible subsets of this set, the contents of which add onto a
predefined value M.
Let there be n elements in the main set. W=w[1..n] represent the
elements of the set. i.e., w = (w1,w2,w3,…,wn) vector x = x[1..n]
assumes either 0 or 1 value. If element w(i) is included in the subset
then x(i) =1.
Consider n=6 m=30 and w[1..6]={5,10,12,13,15,18}. The partial
backtracking tree is shown in fig 6.2. The label to the left of a node
represents the item number chosen for insertion and the label to the
right represents the space occupied in M. S represents a solution to
the given problem and B represents a bounding criteria if no solution
can be reached. For the above problem the solution could be
(1,1,0,0,1,0), (1,0,1,1,0,0) and (0,0,1,0,0,1). Completion of the tree structure is left as an assignment for the reader.
6.3.3 8 queen problem: The 8 queen problem can be stated as follows. Consider a chessboard of order 8X8. The problem is to place 8 queens on this board such that no two queens are attack can attack each other. Illustration.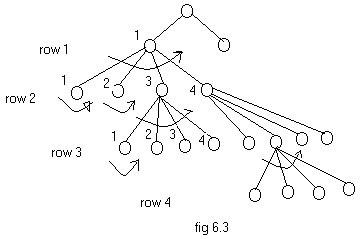
Consider the problem of 4 queens, backtracking solution for this is as
shown in the fig 6.3. The figure shows a partial backtracking tree.
Completion of the tree is left as an assignment for the reader. Post Resume: Click here to Upload your Resume & Apply for Jobs |
|
 IP Logged IP Logged |
|
  |
||
Forum Jump |
You cannot post new topics in this forum You cannot reply to topics in this forum You cannot delete your posts in this forum You cannot edit your posts in this forum You cannot create polls in this forum You cannot vote in polls in this forum |
|
|

© Vyom Technosoft Pvt. Ltd. All Rights Reserved.