4.1 Divide and Conquer

There are a number of general and powerful computational strategies that are repeatedly used in computer science. It is often possible to phrase any problem in terms of these general strategies. These general strategies are Divide and Conquer, Dynamic Programming. The techniques of Greedy Search, Backtracking and Branch and Bound evaluation are variations of dynamic programming idea. All these strategies and techniques are discussed in the subsequent chapters.

The most widely known and often used of these is the divide and conquer strategy. The basic idea of divide and conquer is to divide the original problem into two or more sub-problems which can be solved by the same technique. If it is possible to split the problem further into smaller and smaller sub-problems, a stage is reached where the sub-problems are small enough to be solved without further splitting. Combining the solutions of the individuals we get the final conquering. Combining need not mean, simply the union of individual solutions. Divide and Conquer involves four steps

1. Divide
2. Conquer [Initial Conquer occurred due to solving]
3. Combine
4. Conquer [Final Conquer].

In precise, forward journey is divide and backward journey is Conquer. A general binary divide and conquer algorithm is : Procedure D&C (P,Q) //the data size is from p to q { If size(P,Q) is small Then Solve(P,Q) Else M ¬ divide(P,Q) Combine (D&C(P,M), D&C(M+1,Q)) } Sometimes, this type of algorithm is known as control abstract algorithms as they give an abstract flow. This way of breaking down the problem has found wide application in sorting, selection and searching algorithm. 4.1 Binary Search: Algorithm: m¬ (p+q)/2 If (p £ m £ q) Then do the following Else Stop If (A(m) = Key Then ‘successful’ stop Else If (A(m) < key Then q=m-1; Else p¬ m+1 End Algorithm. Illustration : Consider the data set with elements {12,18,22,32,46,52,59,62,68}. First let us consider the simulation for successful cases. Successful cases: Key=12 P Q m Search 1 9 5 x 1 4 2 x 1 1 1 successful To search 12, 3 units of time is required   Key=18 P Q m Search 1 9 5 x 1 4 2 successful To search 18, 2 units of time is required Key=22 P Q m Search 1 9 5 x 1 4 2 x 3 4 3 successful To search 22, 3 units of time is required Key=32 P Q m Search 1 9 5 x 1 4 2 x 3 4 3 x 4 4 4 successful To search 32, 4 units of time is required Key=46 P Q m Search 1 9 5 successful To search 46, 1 unit of time is required Key=52 P Q m Search 1 9 5 x 6 9 7 x 6 6 6 successful To search 52, 3 units of time is required Key=59 P Q m Search 1 9 5 x 6 9 7 successful To search 59, 2 units of time is required Key=62 P Q m Search 1 9 5 x 6 9 7 x 8 9 8 successful To search 62, 3 units of time is required Key=68 P Q m Search 1 9 5 x 6 9 7 x 8 9 8 x 9 9 9 successful To search 68, 4 units of time is required   3+2+3+4+1+3+2+4 Successful average search time= ------------------------- 9 unsuccessful cases Key=25 P Q m Search 1 9 5 x 1 4 2 x 3 4 3 x 4 4 4 x To search 25, 4 units of time is required       Key=65 P Q m Search 1 9 5 x 6 9 7 x 8 9 8 x 9 9 9 x To search 65, 4 units of time is required 4+4 Unsuccessful search time =-------------------- 2 average (sum of unsuccessful search time search = + sum of Successful search time)/(n+(n+1)) time      

Study Notes Home | Next Section>>

4.1 Divide and Conquer

There are a number of general and powerful computational strategies that are repeatedly used in computer science. It is often possible to phrase any problem in terms of these general strategies. These general strategies are Divide and Conquer, Dynamic Programming. The techniques of Greedy Search, Backtracking and Branch and Bound evaluation are variations of dynamic programming idea. All these strategies and techniques are discussed in the subsequent chapters.

The most widely known and often used of these is the divide and conquer strategy. The basic idea of divide and conquer is to divide the original problem into two or more sub-problems which can be solved by the same technique. If it is possible to split the problem further into smaller and smaller sub-problems, a stage is reached where the sub-problems are small enough to be solved without further splitting. Combining the solutions of the individuals we get the final conquering. Combining need not mean, simply the union of individual solutions. Divide and Conquer involves four steps

1. Divide
2. Conquer [Initial Conquer occurred due to solving]
3. Combine
4. Conquer [Final Conquer].

In precise, forward journey is divide and backward journey is Conquer. A general binary divide and conquer algorithm is : Procedure D&C (P,Q) //the data size is from p to q { If size(P,Q) is small Then Solve(P,Q) Else M ¬ divide(P,Q) Combine (D&C(P,M), D&C(M+1,Q)) } Sometimes, this type of algorithm is known as control abstract algorithms as they give an abstract flow. This way of breaking down the problem has found wide application in sorting, selection and searching algorithm. 4.1 Binary Search: Algorithm: m¬ (p+q)/2 If (p £ m £ q) Then do the following Else Stop If (A(m) = Key Then ‘successful’ stop Else If (A(m) < key Then q=m-1; Else p¬ m+1 End Algorithm. Illustration : Consider the data set with elements {12,18,22,32,46,52,59,62,68}. First let us consider the simulation for successful cases. Successful cases: Key=12 P Q m Search 1 9 5 x 1 4 2 x 1 1 1 successful To search 12, 3 units of time is required   Key=18 P Q m Search 1 9 5 x 1 4 2 successful To search 18, 2 units of time is required Key=22 P Q m Search 1 9 5 x 1 4 2 x 3 4 3 successful To search 22, 3 units of time is required Key=32 P Q m Search 1 9 5 x 1 4 2 x 3 4 3 x 4 4 4 successful To search 32, 4 units of time is required Key=46 P Q m Search 1 9 5 successful To search 46, 1 unit of time is required Key=52 P Q m Search 1 9 5 x 6 9 7 x 6 6 6 successful To search 52, 3 units of time is required Key=59 P Q m Search 1 9 5 x 6 9 7 successful To search 59, 2 units of time is required Key=62 P Q m Search 1 9 5 x 6 9 7 x 8 9 8 successful To search 62, 3 units of time is required Key=68 P Q m Search 1 9 5 x 6 9 7 x 8 9 8 x 9 9 9 successful To search 68, 4 units of time is required   3+2+3+4+1+3+2+4 Successful average search time= ------------------------- 9 unsuccessful cases Key=25 P Q m Search 1 9 5 x 1 4 2 x 3 4 3 x 4 4 4 x To search 25, 4 units of time is required       Key=65 P Q m Search 1 9 5 x 6 9 7 x 8 9 8 x 9 9 9 x To search 65, 4 units of time is required 4+4 Unsuccessful search time =-------------------- 2 average (sum of unsuccessful search time search = + sum of Successful search time)/(n+(n+1)) time

4.2 Max-Min Search

Max-Min search problem aims at finding the smallest as well as the biggest element in a vector A of n elements. Following the steps of Divide and Conquer the vector can be divided into sub-problem as shown below.               The search has now reduced to comparison of 2 numbers. The time is spent in conquering and comparing which is the major step in the algorithm.   Algorithm: Max-Min (p, q, max, min) { If (p = q) Then max = a(p) min = a(q) Else If ( p – q-1) Then If a(p) > a(q) Then max = a(p) min = a(q) Else max = a(q) min = a(p) If End Else m ¬ (p+q)/2 max-min(p,m,max1,min1) max-min(m+1,q,max2,min2) max ¬ large(max1,max2) min ¬ small(min1,min2) If End If End Algorithm End. Illustration 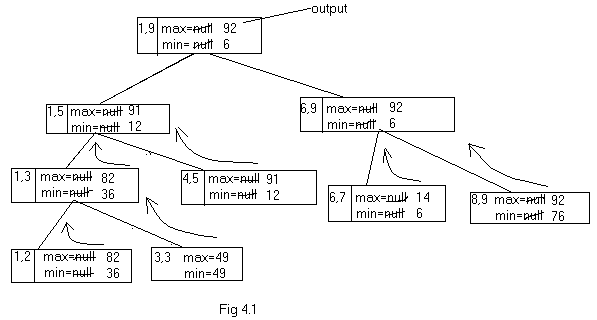    Consider a data set with elements {82,36,49,91,12,14,06,76,92}. Initially the max and min variables have null values. In the first call, the list is broken into two equal halves.. The list is again broken down into two. This process is continued till the length of the list is either two or one. Then the maximum and minimum values are chosen from the smallest list and these values are returned to the preceding step where the length of the list is slightly big. This process is continued till the entire list is searched. The detail description is shown in fig 4.1

4.3 Integer multiplication

There are various methods of obtaining the product of two numbers. The repeated addition method is left as an assignment for the reader. The reader is expected to find the product of some bigger numbers using the repeated addition method. Another way of finding the product is the one we generally use i.e., the left shift method. 4.3.1 left shift method

---

---

981*1234 3924 2943* 1962** 981***

---

1210554 In this method, a=981 is the multiplicand and b=1234 is the multiplier. A is multiplied by every digit of b starting from right to left. On each multiplication the subsequent products are shifted one place left. Finally the products obtained by multiplying a by each digit of b is summed up to obtain the final product. The above product can also be obtained by a right shift method, which can be illustrated as follows, 4.3.2 right shift method

---

---

981*1234

---

981 1962 *2943 **3924

---

1210554 In the above method, a is multiplied by each digit of b from leftmost digit to rightmost digit. On every multiplication the product is shifted one place to the right and finally all the products obtained by multiplying ‘a’ by each digit of ‘b’ is added to obtain the final result. The product of two numbers can also be obtained by dividing ‘a’ and multiplying ‘b’ by 2 repeatedly until a<=1. 4.3.3 halving and doubling method Let a=981 and b=1234 The steps to be followed are

1. If a is odd store b
2. A=a/2 and b=b*2
3. Repeat step 2 and step 1 till a<=1

a	b	result
981	1234	1234
490	2468	------------
245	4936	4936
122	9872	---------
61	19744	19744
30	39488	------------
15	78976	78976
7	157952	157952
3	315904	315904
1	631808	631808

Sum=1210554 The above method is called the halving and doubling method. 4.3.4 Speed up algorithm: In this method we split the number till it is easier to multiply. i.e., we split 0981 into 09 and 81 and 1234 into 12 and 34. 09 is then multiplied by both 12 and 34 but, the products are shifted ‘n’ places left before adding. The number of shifts ‘n’ is decided as follows

Multiplication sequence	shifts
09*12	4	108****
09*34	2	306**
81*12	2	972**
81*34	0	2754

Sum=1210554 For 0981*1234, multiplication of 34 and 81 takes zero shifts, 34*09 takes 2 shifts, 12 and 81 takes 2 shifts and so on. Exercise 4

Write the algorithm to find the product of two numbers for all the methods explained.

Hand simulate the algorithm for atleast 10 different numbers.

Implement the same for verification.

Write a program to find the maximum and minimum of the list of n element with and without using recursion.